Tuesday, 23 December 2014

Lets Learn about size and measurement

December 23, 2014 Nafsiyah No comments

So ...

This Math still cant make you praise Allah SWT ?!

Topic for Final Exam IGCSE Year 9, Number and Probability

December 04, 2014 Year 9 No comments

1.       Expressing number into words, ex: wording of 104256, 1/3, 1/2, ¼ ?
2.       BIDMAS or BODMAS fraction, whole and decimal number?
3.       Converting Unit and estimation
4.       Rounding, ex: 1234 to the nearest 100?
5.       Ordering fraction and percentage
6.       Using calculator for indices
7.       Standard form or scientific form
8.       Converting Currency
9.       Indices rule, (negative, fraction, whole)
10.   Fraction to decimal, fraction to percentage
11.   Speed and time, hour.
12.   Multiple Number
13.   Ratio, proportion
14.   Basic Probability
15.   Percentage loss and fraction loss
16.   Venn diagram & Shading
17.   Sequence and using formula
18.   Probability Tree Diagram

More Detail about Number, and watch the tutorial video click here
Download for speciment paper click here

Try Embedding ppt, word, pdf, excell file

December 03, 2014 Islamic Spark, Nafsiyah, Tsaqofah No comments

Exercise Embedding ppt file

another method for embedding ppt file

Embedding word document

Embedding xls file sheet 1

Embedding xls file whole document

Specimen Paper A level

December 02, 2014 Exam Paper, Year 11, Year 12 No comments

CIE Pure Maths P1 Nov 2013

Sets and Venn Diagram

December 01, 2014 Classroom, Year 10, Year 9 No comments

Sets and Venn Diagrams

Sets

A set is a collection of things.

For example, the items you wear is a set: these would include shoes, socks, hat, shirt, pants, and so on.

You write sets inside curly brackets like this:

{socks, shoes, pants, watches, shirts, ...}

You can also have sets of numbers:

Set of whole numbers: {0, 1, 2, 3, ...}
Set of prime numbers: {2, 3, 5, 7, 11, 13, 17, ...}

Ten Best Friends

You could have a set made up of your ten best friends:

{alex, blair, casey, drew, erin, francis, glen, hunter, ira, jade}

Each friend is an "element" (or "member") of the set (it is normal to use lowercase letters for them.)

Now let's say that alex, casey, drew and hunter play Soccer:

Soccer = {alex, casey, drew, hunter}

(The Set "Soccer" is made up of the elements alex, casey, drew and hunter).

And casey, drew and jade play Tennis:

Tennis = {casey, drew, jade}

You could put their names in two separate circles:

Union

You can now list your friends that play Soccer OR Tennis.

This is called a "Union" of sets and has the special symbol ∪:

Soccer ∪ Tennis = {alex, casey, drew, hunter, jade}

Not everyone is in that set ... only your friends that play Soccer or Tennis (or both).

We can also put it in a "Venn Diagram":

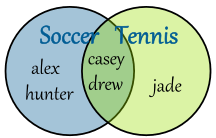
Venn Diagram: Union of 2 Sets

A Venn Diagram is clever because it shows lots of information:

Do you see that alex, casey, drew and hunter are in the "Soccer" set?
And that casey, drew and jade are in the "Tennis" set?
And here is the clever thing: casey and drew are in BOTH sets!

Intersection

"Intersection" is when you have to be in BOTH sets.

In our case that means they play both Soccer AND Tennis ... which is casey and drew.

The special symbol for Intersection is an upside down "U" like this: ∩

And this is how we write it down:

Soccer ∩ Tennis = {casey, drew}

In a Venn Diagram:

Venn Diagram: Intersection of 2 Sets

Which Way Does That "U" Go?

Think of them as "cups": ∪ would hold more water than ∩, right?

So Union ∪ is the one with more elements than Intersection ∩

Difference

You can also "subtract" one set from another.

For example, taking Soccer and subtracting Tennis means people that play Soccer but NOT Tennis ... which is alex and hunter.

And this is how we write it down:

Soccer − Tennis = {alex, hunter}

In a Venn Diagram:

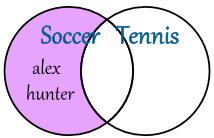
Venn Diagram: Difference of 2 Sets

Summary So Far

∪ is Union: is in either set

∩ is Intersection: must be in both sets

− is Difference: in one set but not the other

Three Sets

You can also use Venn Diagrams for 3 sets.

Let us say the third set is "Volleyball", which drew, glen and jade play:

Volleyball = {drew, glen, jade}

But let's be more "mathematical" and use a Capital Letter for each set:

S means the set of Soccer players
T means the set of Tennis players
V means the set of Volleyball players

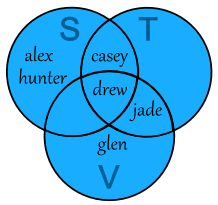
The Venn Diagram is now like this:

Union of 3 Sets: S ∪ T ∪ V

You can see (for example) that:

drew plays Soccer, Tennis and Volleyball
jade plays Tennis and Volleyball
alex and hunter play Soccer, but don't play Tennis or Volleyball
no-one plays only Tennis

We can now have some fun with Unions and Intersections ...

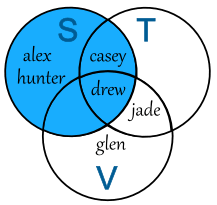
This is just the set S

S = {alex, casey, drew, hunter}

This is the Union of Sets T and V

T ∪ V = {casey, drew, jade, glen}

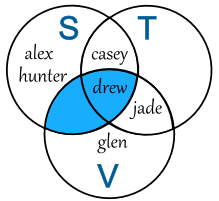
This is the Intersection of Sets S and V

S ∩ V = {drew}

And how about this ...

take the previous set S ∩ V
then subtract T:

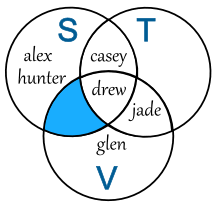
This is the Intersection of Sets S and V minus Set T

(S ∩ V) − T = {}

Hey, there is nothing there!

That is OK, it is just the "Empty Set". It is still a set, so we use the curly brackets with nothing inside: {}

The Empty Set has no elements: {}

Universal Set

The Universal Set is the set that contains everything. Well, not exactlyeverything. Everything that we are interested in now.

Sadly, the symbol is the letter "U" ... which is easy to confuse with the ∪ for Union. You just have to be careful, OK?

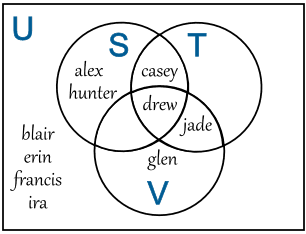
In our case the Universal Set is our Ten Best Friends.

U = {alex, blair, casey, drew, erin, francis, glen, hunter, ira, jade}

We can show the Universal Set in a Venn Diagram by putting a box around the whole thing:

Now you can see ALL your ten best friends, neatly sorted into what sport they play (or not!).

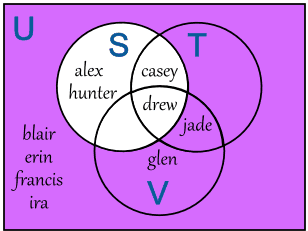
And then we can do interesting things like take the whole set and subtract the ones who play Soccer:

We write it this way:

U − S = {blair, erin, francis, glen, ira, jade}

Which says "The Universal Set minus the Soccer Set is the Set {blair, erin, francis, glen, ira, jade}"

In other words "everyone who does not play Soccer".

Complement

And there is a special way of saying "everything that is not", and it is called "complement".

We show it by writing a little "C" like this:

S^c

Which means "everything that is NOT in S", like this:

S^c = {blair, erin, francis, glen, ira, jade}
(just like the U − C example from above)

Resource:mathisfun.com

Summary

∪ is Union: is in either set

∩ is Intersection: must be in both sets

− is Difference: in one set but not the other

A^c is the Complement of A: everything that is not in A

Empty Set: the set with no elements. Shown by {}

Universal Set: all things we are interested in

Worked Exam Question

Solution

Worksheet
Put all your work on Math Folio Book

Probability Tree Diagrams

December 01, 2014 Classroom, Year 10, Year 9 1 comment

Calculating probabilities can be hard, sometimes we add them, sometimes we multiply them, and often it is hard to figure out what to do ... tree diagrams to the rescue!

Here is a tree diagram for the toss of a coin:

There are two "branches" (Heads and Tails)

The probability of each branch is written on the branch
The outcome is written at the end of the branch

We can extend the tree diagram to two tosses of a coin:

How do we calculate the overall probabilities?

We multiply probabilities along the branches
We add probabilities down columns

Now we can see such things as:

The probability of "Head, Head" is 0.5×0.5 = 0.25
All probabilities add to 1.0 (which is always a good check)
The probability of getting at least one Head from two tosses is 0.25+0.25+0.25 = 0.75
... and more

That was a simple example using independent events (each toss of a coin is independent of the previous toss), but tree diagrams are really wonderful for figuring out dependent events (where an event depends on what happens in the previous event) like this example:

Example: Soccer Game

You are off to soccer, and love being the Goalkeeper, but that depends who is the Coach today:

with Coach Sam the probability of being Goalkeeper is 0.5
with Coach Alex the probability of being Goalkeeper is 0.3

Sam is Coach more often ... about 6 out of every 10 games (a probability of 0.6).

So, what is the probability you will be a Goalkeeper today?

Let's build the tree diagram. First we show the two possible coaches: Sam or Alex:

The probability of getting Sam is 0.6, so the probability of Alex must be 0.4 (together the probability is 1)

Now, if you get Sam, there is 0.5 probability of being Goalie (and 0.5 of not being Goalie):

If you get Alex, there is 0.3 probability of being Goalie (and 0.7 not):

The tree diagram is complete, now let's calculate the overall probabilities. This is done by multiplying each probability along the "branches" of the tree.

Here is how to do it for the "Sam, Yes" branch:

(When we take the 0.6 chance of Sam being coach and include the 0.5 chance that Sam will let you be Goalkeeper we end up with an 0.3 chance.)

But we are not done yet! We haven't included Alex as Coach:

An 0.4 chance of Alex as Coach, followed by an 0.3 chance gives 0.12.

Now we add the column:

0.3 + 0.12 = 0.42 probability of being a Goalkeeper today

(That is a 42% chance)

Check

One final step: complete the calculations and make sure they add to 1:

0.3 + 0.3 + 0.12 + 0.28 = 1

Yes, it all adds up.

Conclusion

So there you go, when in doubt draw a tree diagram, multiply along the branches and add the columns. Make sure all probabilities add to 1 and you are good to go.