Entering Higher Education with Cambridge International As and A Level

resource : CIE, British Council, Education USA, Australian Embassy

Read More

Are You Math Phobia?

For a lot of people, MATH is the abbreviation for ‘Mental Abuse To Humans’. You must have heard of it too, right? Well, it’s not true. Maths is a scoring subject and the only way to learn Mathematics is to do Mathematics. If you can’t relate interesting word with Maths, then sorry to say but you too belong to the ‘Maths Phobic’ club. Fight the fear of Math today and score well tomorrow. Here’s how:

1. Explore new learning options

If you’re sick of old, heavy and bulky Maths books Learn Maths with educational tablets. Educational DVDs, CDs and Pen Drives are next on the list. Such educational devices feature advanced learning modules and come pre-loaded with rich content library and assessment tools. These tools facilitate learning from attractive illustrations, examples, diagrams, presentations, charts, animation etc. You can find a number of Maths Apps for your smartphone on Google and learn as per your convenience anytime and anywhere!

2. Try out with friends

For most students, Maths is hard and often uninteresting. If you are one of them, you can add a fun element to your learning by solving math problems with your friends. Talk about problems, compete with each other and assess each other’s performance. You’ll find it more helpful than sitting in your room alone and fighting with Algebra, Trigonometry or Integration.

3. Read every problem completely

Many a time important information goes unnoticed when you read a problem just for the sake of getting an answer. Glancing hastily and starting calculations often lead to wrong answers. Efforts and time, all in vain! To avoid this, pen down every given value and figure out what is required. If you find the question complicated, read it again.

4. Change the words

Whenever you find any Math problem boring, make it a little interesting for yourself. Try changing names, words, etc. just to hold your interest in the problem. Never change the original numbers in your problem when changing words. This might lead to wrong answers and a heavy disappointment.

5. Understand by drawing

Be a little creative! If possible, try to understand problems by drawing diagrams. This really helps in understanding exactly what the question is asking making it easier to find a solution.

6. Practice makes a man perfect

Math demands practice. After you are finished with your text book learning, use reference books to solve more questions. This will help in confidence building and will make certain concepts more clear.

Read More

Radian, length and area of sector

Math A level Syllabus, 2016

Circle

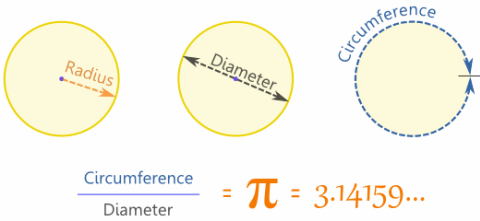
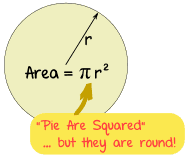
A circle is easy to make: Draw a curve that is "radius" away from a central point. And so: All points are the same distance from the center.

You Can Draw It Yourself

Put a pin in a board, put a loop of string around it, and insert a pencil into the loop. Keep the string stretched and draw the circle!

Radius, Diameter and Circumference

The Radius is the distance from the center to the edge.

The Diameter starts at one side of the circle, goes through the center and ends on the other side.

The Circumference is the distance around the edge of the circle.

And here is the really cool thing:

When we divide the circumference by the diameter we get 3,141592654...
which is the number π (Pi)

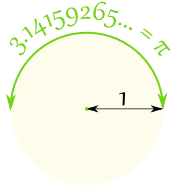
So when the diameter is 1, the circumference is 3,141592654...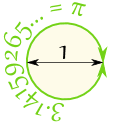

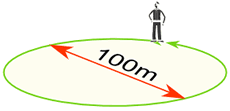We can say:

Circumference = π × Diameter

Example: You walk around a circle which has a diameter of 100m, how far have you walked?

Distance walked = Circumference = π × 100m = 314m (to the nearest m)

Also note that the Diameter is twice the Radius:

Diameter = 2 × Radius

And so this is also true:

Circumference = 2 × π × Radius

Remembering

The length of the words may help you remember:

• Radius is the shortest word
• Diameter is longer (and is 2 × Radius)
• Circumference is the longest (and is π × Diameter)

Definition

The circle is a plane shape (two dimensional): And the definition of a circle is:

The set of all points on a plane that are a fixed distance from a center.

Area

The area of a circle is π times the radius squared, which is written:

A = π r²

To help you remember think "Pie Are Squared"
(even though pies are usually round)

Or, using the Diameter:

A = (π/4) × D²

Example: What is the area of a circle with radius of 1,2 m ?

A = π × r²

A = π × 1,2²

A = π × (1,2 × 1,2)

A = 3,14159... × 1,44 = 4,52 (to 2 decimals)

Area Compared to a Square

A circle has about 80% of the area of a similar-width square.
The actual value is (π/4) = 0,785398... = 78,5398...%

Names

Because people have studied circles for thousands of years special names have come about.

Nobody wants to say "that line that starts at one side of the circle, goes through the center and ends on the other side" when a word like "Diameter" will do.

So here are the most common special names:

Lines

A line that goes from one point to another on the circle's circumference is called a Chord.

If that line passes through the center it is called a Diameter.

A line that "just touches" the circle as it passes by is called aTangent.

And a part of the circumference is called an Arc.

Slices

There are two main "slices" of a circle. The "pizza" slice is called a Sector. And the slice made by a chord is called a Segment.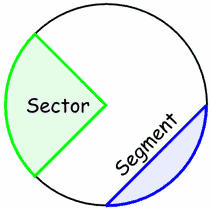

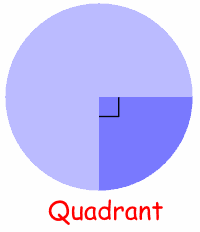Common Sectors

The Quadrant and Semicircle are two special types of Sector:

	Quarter of a circle is called a Quadrant. Half a circle is called a Semicircle.

Inside and Outside

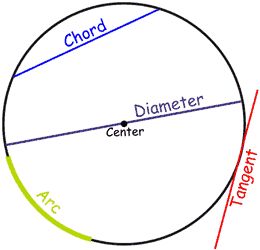
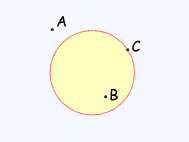A circle has an inside and an outside (of course!). But it also has an "on", because we could be right on the circle. Example: "A" is outside the circle, "B" is inside the circle and "C" is on the circle.

Radians

The angle made when we take the radius and
wrap it along the edge of the circle:

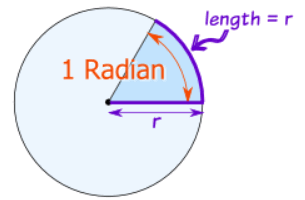
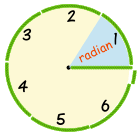
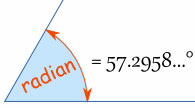1 Radian is about 57,2958 degrees.

Why "57,2958..." degrees? We will see in a moment.

The Radian is a pure measure based on the Radius of the circle:

Radian: the angle made when we take the radius
and wrap it along the edge of a circle.

Radians and Degrees

Let us see why 1 Radian is equal to 57,2958... degrees:

In a half circle there are π radians, which is also 180°

So:		π radians	=	180°
So:		1 radian	=	180°/π
			=	57,2958...°
				(approximately)

To go from radians to degrees: multiply by 180, divide by π

To go from degrees to radians: multiply by π, divide by 180

Here is a table of equivalent values:

Degrees	Radians (exact)	Radians (approx)
30°	π/6	0,524
45°	π/4	0,785
60°	π/3	1,047
90°	π/2	1,571
180°	π	3,142
270°	3π/2	4,712
360°	2π	6,283

Example: How Many Radians in a Full Circle?

Imagine you cut up pieces of string exactly the length from thecenter of a circle to its edge ...

... how many pieces do you need to go around the edge of the circle?

Answer: 2π (or about 6,283 pieces of string).

Radians Preferred by Mathematicians

Because the radian is based on the pure idea of "the radius being laid along the circumference", it often gives simple and natural results when used in mathematics.

For example, look at the sine function for very small values:

x (radians)	1	0,1	0,01	0,001
sin(x)	0,8414710	0,0998334	0,0099998	0,0009999998

For very small values. "x" and "sin(x)" are almost the same
(as long as "x" is in Radians!)

There will be other examples like that as you learn more about mathematics.

Conclusion

So, degrees are easier to use in everyday work, but radians are much better for mathematics.

Circle Sector and Segment

Slices There are two main "slices" of a circle: The "pizza" slice is called a Sector. And the slice made by a chord is called a Segment.

Try Them!

Sector	Segment

Common Sectors

The Quadrant and Semicircle are two special types of Sector:

Half a circle is
a Semicircle.

Quarter of a circle is
a Quadrant.

Area of a Sector

You can work out the Area of a Sector by comparing its angle to the angle of a full circle.

Note: we are using radians for the angles.

This is the reasoning:

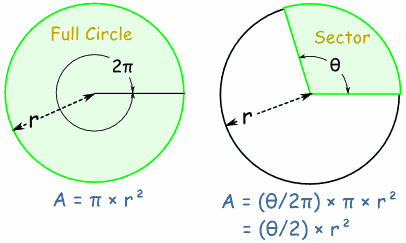
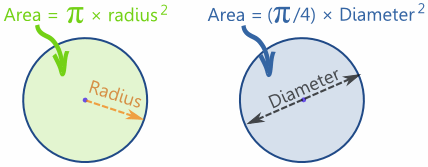
A circle has an angle of 2π and an Area of:		πr2
A Sector with an angle of θ (instead of 2π) has an Area of:		(θ/2π) × πr2
Which can be simplified to:		(θ/2) × r2

Area of Sector = ½ × θ × r²   (when θ is in radians)

Area of Sector = ½ × (θ × π/180) × r²   (when θ is in degrees)

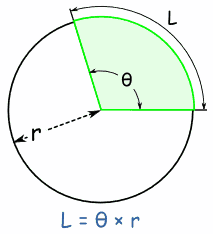Arc Length By the same reasoning, the arc length (of a Sector or Segment) is: L = θ × r   (when θ is in radians) L = (θ × π/180) × r   (when θ is in degrees)

Area of Segment The Area of a Segment is the area of a sector minus the triangular piece (shown in light blue here). There is a lengthy reason, but the result is a slight modification of the Sector formula: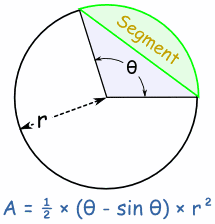
Area of Segment = ½ × (θ - sin θ) × r2   (when θ is in radians) Area of Segment = ½ × ( (θ × π/180) - sin θ) × r2   (when θ is in degrees)

resource : www.mathisfun.com


exercise 1



Exercise 2

Read More

Building Good Habit

	Habit 1 — Be Proactive You're in Charge I am a responsible person. I take initiative. I choose my actions, attitudes, and moods. I do not blame others for my wrong actions. I do the right thing without being asked, even when no one is looking.
	Habit 2 — Begin With the End in Mind Have a Plan I plan ahead and set goals. I do things that have meaning and make a difference. I am an important part of my classroom and contribute to my school’s mission and vision. I look for ways to be a good citizen.
	Habit 3 — Put First Things First Work First, Then Play I spend my time on things that are most important. This means I say no to things I know I should not do. I set priorities, make a schedule, and follow my plan. I am disciplined and organized.
	Habit 4 — Think Win-Win Everyone Can Win I balance courage for getting what I want with consideration for what others want. I make deposits in others’ Emotional Bank Accounts. When conflicts arise, I look for Third Alternatives.
	Habit 5 — Seek First to Understand, Then to Be Understood Listen Before You Talk I listen to other people’s ideas and feelings. I try to see things from their viewpoints. I listen to others without interrupting. I am confident in voicing my ideas. I look people in the eyes when talking.
	Habit 6 — Synergize Together Is Better I value other people’s strengths and learn from them. I get along well with others, even people who are different from me. I work well in groups. I seek out other people’s ideas to solve problems because I know that by teaming with others, we can create better solutions than anyone of us can alone. I am humble.
	Habit 7 — Sharpen the Saw Balance Feels Best I take care of my body by eating right, exercising, and getting sleep. I spend time with family and friends. I learn in lots of ways and lots of places, not just at school. I find meaningful ways to help others.

Read More